Defining Tasks and Developing Schedules
Defining and Sequencing Tasks – The NASA Systems Engineering Handbook discusses in section 4.4 the use of work flow diagrams (WFD) for developing schedules. The WFD is a graphical representation of tasks, task precedencies or dependencies and “products or milestones” that occur as a result of one or more tasks. Using the WFD as defined can lead to scheduling problems due to not fully defining each task. It’s possible to expand the definition of the WFD so that tasks are fully defined. However, there is a simple tool for more completely defining and sequencing tasks that can be used in conjunction with or independently of the WFD before any schedule below the top level is developed.
A simple and effective tool for defining and sequencing detailed tasks is the N-Squared diagram. N-Squared diagrams are traditionally used in defining software and hardware interfaces but are just as valuable for defining interfaces between tasks. N-Squared diagrams are constructed for tasks and subtasks as a nested set using spreadsheet tools. Tasks are listed in squares along the diagonal set of squares in an N x N matrix of squares. In addition to putting the task name in a diagonal square other information useful to the project team can be added; e.g. the Work Breakdown Structure (WBS) number of the task, or perhaps the task leader’s name, or a paragraph number in a proposal or task description document that describes the task.
N-Squared diagrams can be developed top down or bottoms up or using a mix of bottoms up and top down. Here it is described as a top down process but don’t be constrained by this description. Start with a list of N tasks of the same level in the order you think they need to be executed. Top level tasks often have multiple levels of subtasks. List each top level task in turn in one of the squares along the diagonal of the N x N matrix. The N-Squared diagrams for the subtasks of each task are constructed as separate diagrams.
The next step is to write the external inputs to the tasks in the row above the diagram and above the square containing the task that the external inputs feed into. Then write the outputs of the first task in squares that are to the right of the first square in the first row of squares. Each output is to be in the square directly above the diagonal square containing the task that requires the output from the first task as an input. Then continue this process for each diagonal square. Outputs that feed tasks in diagonal squares that are above the row go in boxes to the left of the diagonal square and outputs that feed tasks in diagonal squares that are below the row go in boxes to the right of the diagonal square. This process defines the tasks in that the inputs and outputs of each task are identified along with the sources of the inputs and the tasks that need the outputs.
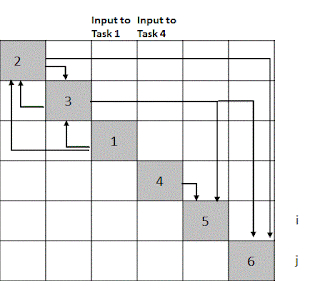
After completing this listing of outputs for each diagonal square examine the form of the resulting N x N matrix. A simple example with six tasks, one external input to task 1 and two outputs from tasks five and six is shown in Figure 4-1. In this figure the tasks are labeled with numbers along the diagonal and the outputs from tasks are labels with letters. Arrows can be added to make it clear which task each output feeds, as shown in Figure 4-1.
Figure 4-1 An N-Square diagram is a useful tool for defining tasks and the relationships between tasks.
An ideal sequence of tasks for a perfectly sequential project has outputs only to the right side of the diagonal. Typical projects have some tasks with outputs on the left of the diagonal squares. These outputs represent feedbacks to earlier tasks. Typically in executing the tasks in the diagonal squares that have feedbacks from tasks in squares in lower level squares assumptions or estimates are made for the inputs needed from lower level tasks and the tasks are reviewed or repeated after the lower level tasks are completed. Thus the form of the N x N diagram defines how efficiently the tasks are ordered. If there are a lot of outputs on the left side of the diagonal it is necessary to see if reordering the tasks results in moving more outputs to the right of the diagonal and thereby reducing the number of feedback loops that must be executed. Executing feedback loops increases the time and cost for completing the work. Therefore sequencing the tasks for a minimum number of feedback loops usually means achieving a task sequence that leads to the least rework, the shortest schedule and the lowest cost.
Often it is easy to get the top level summery tasks in the most efficient order even without using an N x N diagram. The value of this tool comes in sequencing lower level tasks. Once the top level tasks are sequenced then prepare N-Squared diagrams for each of the top level tasks. For example, suppose one of the top level tasks is System Trade Studies. Complex systems can have a dozen to several dozen system trades that are highly interrelated. It takes only a few hours to define the best order for the trades using an N-Squared diagram. Having just one or two tasks out of order can increase the time for completing all trades by days or even weeks.
Figure 4-2 illustrates an N-Squared diagram for the tasks defined in Figure 4-1 with task 1 sequenced to follow tasks 2 and 3. In this figure only arrows are used to indicate outputs from tasks and where the outputs are needed to make it easier to see the effects of sequencing errors. The sequence in Figure 4-2 is obviously less desirable than that of Figure 4-1 because there are multiple feedbacks, which increases the time needed to execute these six tasks compared to the time for the sequence shown in Figure 4-1.
Figure 4-2 This sequence has three outputs to the left of the diagonal compared to one for the sequence shown in Figure 4-1 and therefore takes more time to execute all six tasks.
There is a second payoff from constructing an N-Squared diagram. The form of the diagram not only defines the most efficient sequence for tasks it also shows which tasks can be conducted in parallel. For example, note that task four has externally available input data and requires no data from any of the first three tasks. Thus the fourth task can be started in parallel with the first task, or at any time such that its output is available at the start of task five. Obviously tasks can be started as soon as the necessary inputs from earlier tasks are available and staff is available to execute the task. For example, in Figure 4-1 if there was no output from task 3 feeding to task 6 then task 6 could be executed any time after task 2 and the repeat of task 2 with data from task 3 is complete. The form of the N-Square diagram reveals immediately all tasks that can be started in parallel. Starting tasks in parallel increases the flexibility in staffing. Achieving maximum schedule flexibility, i.e. maximum lead and lag times for tasks, should be one of the goals of scheduling tasks.
To avoid the rework resulting from too much detailed task planning and scheduling in the initial project planning effort prepare second and third level N-Squared diagrams for only those top level tasks that are likely to be executed in the first two to four months of the project. Second and third level diagrams for summary tasks that are to be executed later should be developed with sufficient lead time before these tasks are to begin to allow for planning the staffing of the upcoming tasks.
Finally, N-Squared diagrams are often a very useful visual aid to communicate to customers and managers the scope and status of project work. A skilled project manager on a satellite program posted a project N-Squared diagram where it could be easily reviewed by customers and team members. He colored tasks to show task completions so that status was communicated at a glance. This gave the customers increased confidence in the project team and project management compared to just seeing schedule charts.
Developing the Schedule – This discussion assumes that those responsible for developing the schedule are familiar with both the principles of network scheduling, such as Program Evaluation and Review Technique (PERT) or Critical Path Method (CPM), and are skilled in using modern scheduling software tools. This material is not intended to teach scheduling but systems engineers need to be aware of some pitfalls in scheduling complex projects. A recommendation for the inexperienced scheduler is to study a text book on scheduling projects. James B. Dilworth’s “Production and Operations Management” contains an excellent discussion of scheduling. Particularly important is Dilworth’s discussion of PERT using probabilistic time estimates. An alternative view of probabilistic schedules is found on the web in a blog post by Glen B. Alleman and should be studied by anyone involved in scheduling complex projects. Finally read Eliyahu M. Goldratt’s book “Critical Chain” or search “Critical Chain” on the web and read about Critical Chain Project Management (CCPM). The NASA Systems Engineering Handbook has a description of a process to develop a network schedule after finishing work flow diagrams or N-Squared diagrams. This description isn’t repeated here but a couple of comments are needed.
First, the NASA process calls for a bottom up approach; lower level tasks for subsystems or other work products are scheduled and then these groups of tasks are integrated in the scheduling tool to form the complete detail schedule. This can lead to difficulties and a lot of rework. The rework process is described in the NASA Handbook but much of the rework can be avoided by developing the detail schedule top down.
Typically projects have schedule constraints and developing the schedule bottom up leaves to the end the work of making the complete schedule comply with the constraints where it becomes complex and error prone. It is recommended that when a project has schedule constraints or when the project team wants to meet fixed dates for major milestones and deliveries then include these constraint dates on the Master schedule. Then develop the detail schedule top down from the Master schedule. Scheduling tools can combine these two schedules into what truly can be called an integrated master schedule (IMS).
The top down approach works best if the persons developing the schedule meet with those knowledgeable of the work needed at lower levels and work out the details necessary to comply with the constraints. This is time consuming but actually takes less time than it does to fix a complete schedule that doesn’t meet constraints. Plus, the bottom up approach nearly always results in having to go back to those responsible for the lower level tasks and rework the task details. This is aggravating to workers and managers.
Second, the NASA process does not discuss the variability of task durations and probabilistic scheduling that accounts for this variability. Probabilistic scheduling is most important for accurately determining the critical path. Probabilistic scheduling is discussed in a later section on critical path analysis.

No comments:
Post a Comment